Abstract
The generation of optimal trajectories for high-dimensional robotic systems under constraints remains computationally challenging due to the need to simultaneously satisfy dynamic feasibility, input limits, and task-specific objectives while searching over high-dimensional spaces. Recent approaches using the Affine Geometric Heat Flow (AGHF) Partial Differential Equation (PDE) have demonstrated promising results, generating dynamically feasible trajectories for complex systems like the Digit V3 humanoid within seconds. These methods efficiently solve trajectory optimization problems over a two-dimensional domain by evolving an initial trajectory to minimize control effort. However, these AGHF approaches are limited to a single type of optimal control problem (i.e., minimizing the integral of squared control norms) and typically require initial guesses that satisfy constraints to ensure satisfactory convergence. These limitations restrict the potential utility of the AGHF PDE especially when trying to synthesize trajectories for robotic systems. This paper generalizes the AGHF formulation to accommodate arbitrary cost functions, significantly expanding the classes of trajectories that can be generated. This work also introduces a Phase 1 - Phase 2 Algorithm that enables the use of constraint-violating initial guesses while guaranteeing satisfactory convergence. The effectiveness of the proposed method is demonstrated through comparative evaluations against state-of-the-art techniques across various dynamical systems and challenging trajectory generation problems.
Approach

It begins with an initial trajectory (shown in orange with the color gradient illustrating the evolution in time starting from darkest and going to lightest) that may violate constraints (e.g., the second and fourth pose of the arm are in collision with the boxes and outlined in red). If the initial trajectory is infeasible, BLAZE enters Phase 1, where it evolves the trajectory into a trajectory that satisfies all constraints (e.g., in the blue trajectory, the Kinova arm has been moved out of collision with the boxes). Once the trajectory satisfies all constraints, Phase 2 begins, optimizing the motion to minimize a user-specified cost function while maintaining feasibility (optimized trajectory shown green). In this case, BLAZE optimizes the trajectory to reach a target configuration while avoiding the obstacles while considering the full dynamical model of the arm. Note that optimal control (including Phase 1 and Phase 2) for this 14 dimensional state space model is completed within \(3\)s while satisfying input, state, and collision avoidance constraints.
This paper’s contributions are three-fold:
- This paper illustrates how to formulate the AGHF Action Functional to solve optimal control problems with arbitrary cost functions
- This paper illustrates how to implement a Phase 1-Phase 2 style method that enables the AGHF initial guess to violate the constraints while still generating feasible solutions rapidly;
- This paper describes a computationally tractable formulation to enforce input constraints in the AGHF without increasing the system’s state dimension
Results
BLAZE Solve Time Comparison
This section shows the solve of BLAZE against comparison methods RAPTOR, Crocoddyl and Aligator. In each of these trials input and joint limits are enforced, but there are no obstacle avoidance constraints. The results show the time each method takes to solve a fixed time swing up problem for a 1-, 2-, 3-, 4-, and 5-link pendulum model (N = 1 to 5), a fixed time and final state specified trajectory optimization for the Kinova arm (N = 7), a bimanual manipulator system comprised of two Kinova arms (N = 14) and a trimanual manipulator system comprised of three Kinova arms (N = 21).
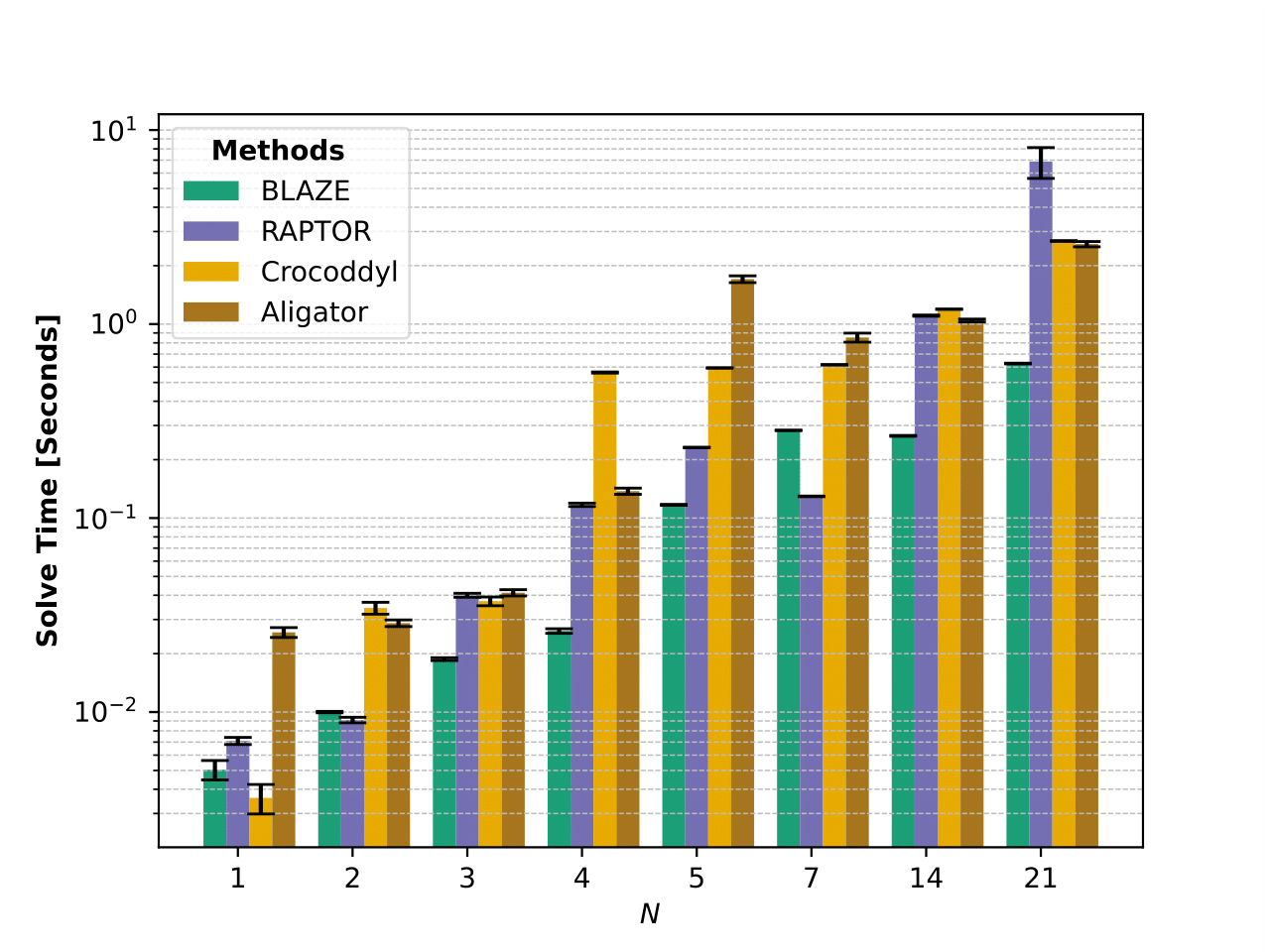
The bar plot above compares the mean solve times for the four different trajectory generation algorithms: BLAZE, RAPTOR, Crocoddyl and Aligator. Each experiment was run ten times. Overall, we see that BLAZE shows better empirical scalability and solve times than the other methods as the system dimension increases.
Kinova Simulation Obstacle Avoidance Results
The following videos demonstrate the various trajectories generated by BLAZE for the 7DOF Kinova Gen3 to navigate from the start configuration to the goal configuration while avoiding obstacles (red). In each scenario, the initial guess trajectory is shown with its start/end in shades of orange, while the optimized solution trajectory is shown with its start/end in shades of green. In each video the different color shades illustrate the evolution in time where the start configuration is in the darkest shade and the end configuration in the lightest. These initial guess trajectories collide with obstacles along their path, but BLAZE is able to push these initial guesses out of collision and generate the optimal collision-free solutions. All of these collision-free trajectories were generated in ≤ 3 seconds
Initial Guess Trajectory
Solution Trajectory
Kinova Hardware Obstacle Avoidance
Hardware scenario 1 (Solved in 3.1 seconds)
Initial Guess
Solution on Hardware
Hardware scenario 2 (Solved in 2.74 seconds)
Initial Guess
Solution on Hardware
Hardware scenario 3 (Solved in 2.45 seconds)
Citation
This project was developed in Robotics and Optimization for Analysis of Human Motion (ROAHM) Lab at the University of Michigan - Ann Arbor.
@ARTICLE{enninfulchuquiureblaze2025,
title={Phasing Through the Flames: Rapid Motion Planning with the AGHF PDE for Arbitrary Objective Functions and Constraints},
author={Challen Enninful Adu and César E. Ramos Chuquiure and Yutong Zhou and Pearl Lin and Ruikai Yang and Bohao Zhang and Shubham Singh and Ram Vasudevan},
year={2025},
eprint={2505.01589},
archivePrefix={arXiv},
primaryClass={cs.RO},
url={https://arxiv.org/abs/2505.01589},
}