Digit Doing Yoga Pose (Generated in ~3s)
Digit Stepping on Box (Generated in ~2s)
Abstract
Generating optimal trajectories for high-dimensional robotic systems in a time-efficient manner while adhering to constraints is a challenging task. To address this challenge, this paper introduces PHLAME, which applies pseudospectral collocation and spatial vector algebra to efficiently solve the Affine Geometric Heat Flow (AGHF) Partial Differential Equation (PDE) for trajectory optimization. Unlike traditional PDE approaches like the Hamilton-Jacobi-Bellman (HJB) PDE, which solve for a function over the entire state space, computing a solution to the AGHF PDE scales more efficiently because its solution is defined over a two-dimensional domain, thereby avoiding the intractability of state-space scaling. To solve the AGHF one usually applies the Method of Lines (MOL), which works by discretizing one variable of the AGHF PDE, effectively converting the PDE into a system of ordinary differential equations (ODEs) that can be solved using standard time-integration methods. Though powerful, this method requires a fine discretization to generate accurate solutions and still requires evaluating the AGHF PDE which can be commputationally expensive for high dimensional systems. PHLAME overcomes this deficiency by using a pseudospectral method, which reduces the number of function evaluations required to yield a high accuracy solution thereby allowing it to scale efficiently to high-dimensional robotic systems. To further increase computational speed, this paper presents analytical expressions for the AGHF and its Jacobian, both of which can be computed efficiently using rigid body dynamics algorithms. The proposed method PHLAME is tested across various dynamical systems, with and without obstacles and compared to a number of state-of-the-art techniques. PHLAME is able to generate trajectories for a 44-dimensional state-space system in ~5 seconds, much faster than current state-of-the-art techniques. Code is available on GitHub at roahmlab/PHLAME.
Approach
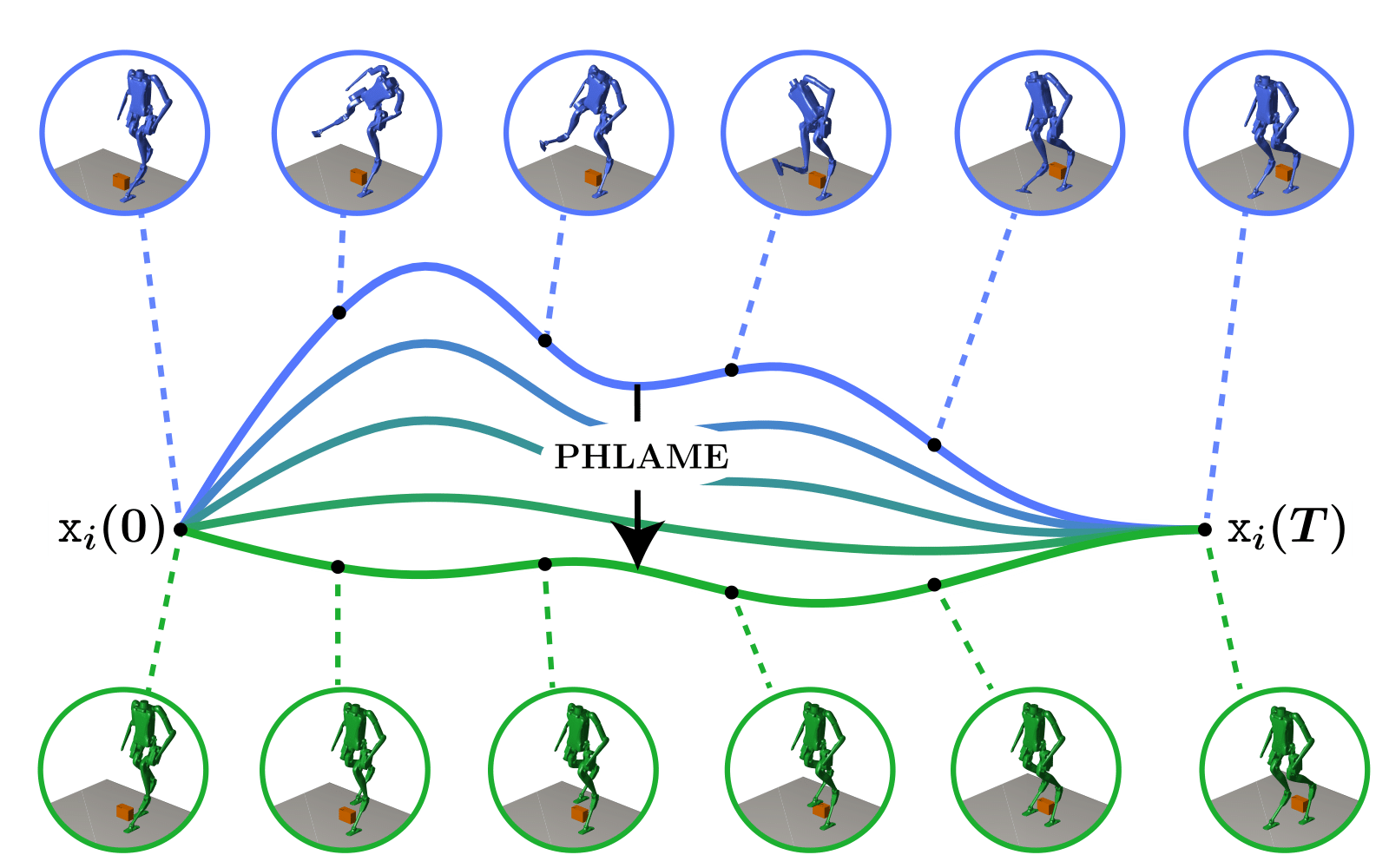
To address the limitations of existing approaches, this paper proposes Pseudospectral Heat fLow using the Affine geoMetric heat flow Equation (PHLAME). The proposed method applies pseudospectral collocation and spatial vector algebra to efficiently solve the Affine Geometric Heat Flow (AGHF) Partial Differential Equation (PDE) enabling rapid trajectory optimization for high dimensional systems. PHLAME works by first taking in some initial guess of a trajectory (shown in dark blue) which does not have to be dynamically feasible and evolves it into some dynamically feasible final trajectory (shown in dark green). Both trajectories start and end at \(\mathtt{x}(0) = \mathtt{x}_0\) and \(\mathtt{x}(T) = \mathtt{x}_f\) respectively. Notice that at the initial trajectory Digit has a dynamically infeasible set of configurations during it’s stepping trajectory and that at the end of the PHLAME solve that trajectory is made into a dynamically feasible one where Digit is able to step over the box.
This paper’s contributions are four-fold:
- A pseudospectral method that reduces the number of AGHF evaluations and nodes when compared to the classical MOL, which allows PHLAME to scale up to high dimensional robotic systems;
- An analytical expression for the AGHF in terms of the rigid body dynamics equation and an algorithm to rapidly evaluate this analytical AGHF expression using spatial vector algebra based rigid body dynamics algorithms;
- An analytical expression for the jacobian of the AGHF and an algorithm to rapidly compute it using spatial vector algebra based rigid body dynamics algorithms;
- A demonstration that PHLAME generating trajectories for a number of different high-dimensional robots systems with and without constraints in a few seconds, much faster that other state-of-the-art trajectory optimization methods
Results
PHLAME Solve Time Comparison
This section shows the solve of PHLAME against comparison methods Crocoddyl and Original AGHF. The results show the time each method takes to solve a fixed time swing up problem for a 1-, 2-, 3-, 4-, and 5-link pendulum model (N = 1 to 5), a fixed time and final state specified trajectory optimization for the Kinova arm (N = 7), and a fixed time and final state trajectory optimization having the pinned Digit execute a step (N = 22).
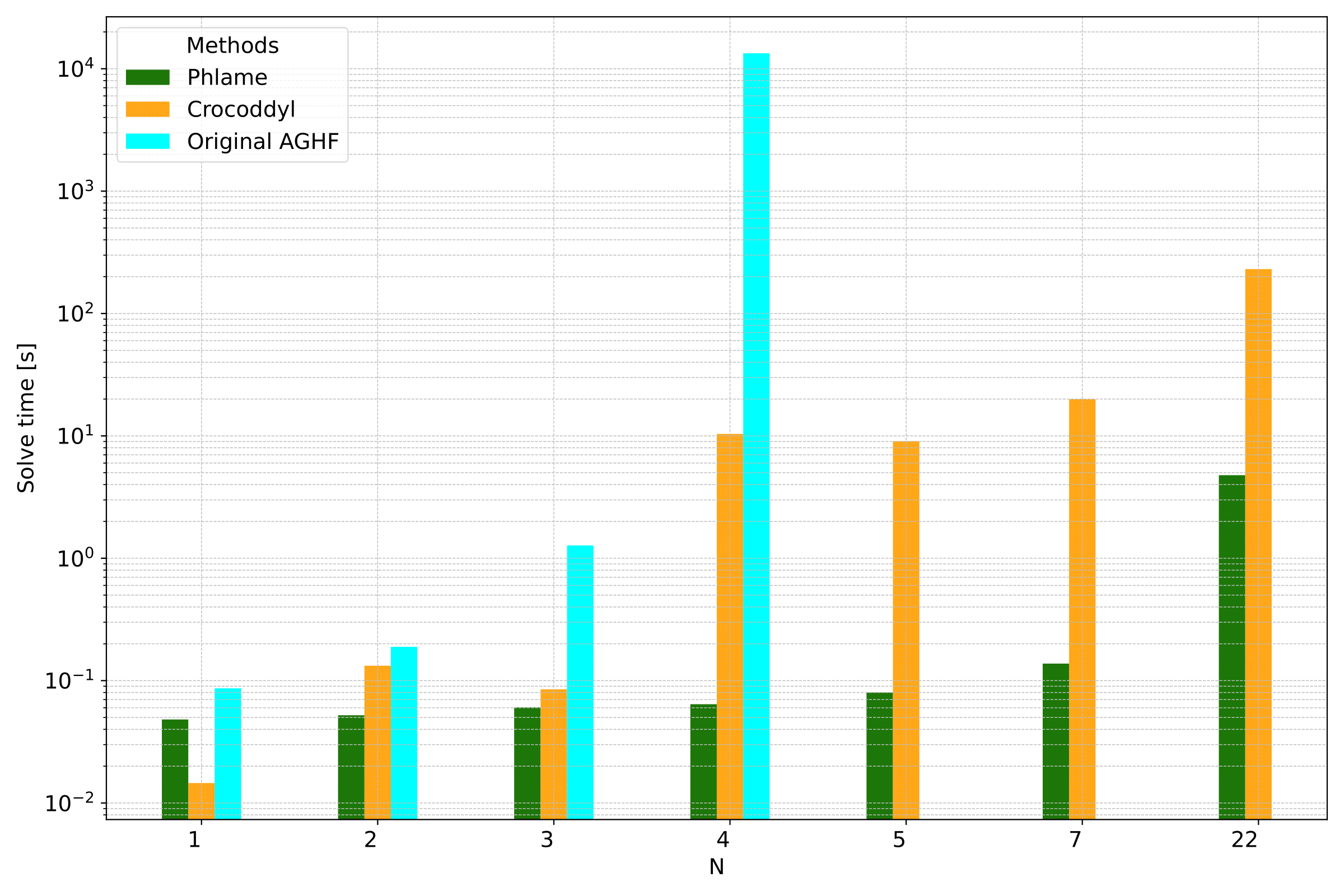
The bar plot above compares the mean solve times for the three different trajectory generation algorithms: PHLAME, AGHF and Crocoddyl. Each experiment was run ten times using the best solver parameter set. For \(N>=5\) we do not show results for the Original AGHF implementation as no results were obtained in a reasonable amount of time. Overall, we see that PHLAME shows better empirical scalability and solve time than the other methods.
Kinova Obstacle Avoidance Scenarios
The following videos demonstrate the various trajectories generated by PHLAME for the 7DOF Kinova Gen3 to navigate from the start configuration (turqoise) to the goal configuration (gold) while avoiding obstacles (red). All of these trajectories were generated in < 0.3 seconds
Digit Scenarios
The following videos demonstrate various trajectories generated by PHLAME for the 22DOF Pinned Digit V3 to navigate from the start configuration (turqoise) to the goal configuration (gold). All of these trajectories were generated in < 5 seconds
Citation
This project was developed in Robotics and Optimization for Analysis of Human Motion (ROAHM) Lab at the University of Michigan - Ann Arbor.
@ARTICLE{enninfulphlame2024,
author={Adu, Challen Enninful and Chuquiure, César E. Ramos and Zhang, Bohao and Vasudevan, Ram},
journal={IEEE Robotics and Automation Letters},
title={Bring the Heat: Rapid Trajectory Optimization With Pseudospectral Techniques and the Affine Geometric Heat Flow Equation},
year={2025},
volume={10},
number={4},
pages={4148-4155},
keywords={Heuristic algorithms;Heating systems;Robots;Trajectory optimization;Vectors;Partial differential equations;Dynamic programming;Planning;Optimal control;Faces;Optimization and optimal control;motion and path planning;integrated planning and control},
doi={10.1109/LRA.2025.3547299}}