Overview Video
Abstract
A key challenge to ensuring the rapid transition of robotic systems from the industrial sector to more ubiquitous applications is the development of algorithms that can guarantee safe operation while in close proximity to humans. Motion planning and control methods, for instance, must be able to certify safety while operating in real-time in arbitrary environments and in the presence of model uncertainty. This paper proposes Wrench Analysis for Inertial Transport using Reachability (WAITR), a certifiably safe motion planning and control framework for serial link manipulators that manipulate unsecured objects in arbitrary environments. WAITR uses reachability analysis to construct over-approximations of the contact wrench applied to unsecured objects, which captures uncertainty in the manipulator dynamics, the object dynamics, and contact parameters such as the coefficient of friction. An optimization problem formulation is presented that can be solved in real-time to generate provably-safe motions for manipulating the unsecured objects. This paper illustrates that WAITR outperforms state of the art methods in a variety of simulation experiments and demonstrates its performance in the real-world.
Method
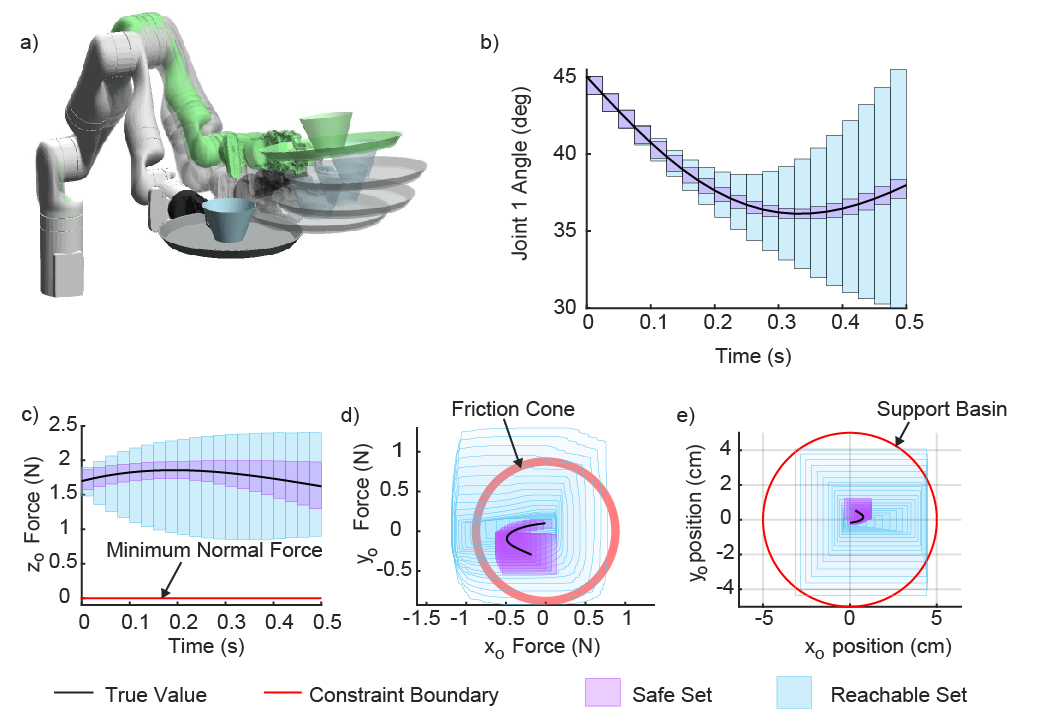
This paper considers the problem of safe motion planning for manipulation of unsecured objects with uncertain dynamics such as manipulating an unsecured cup filled with an uncertain mass around randomly placed obstacles (red) such that the cup does not move relative to the tray supporting it. WAITR operates in receding-horizon fashion, moving from a start configuration (blue) to a global goal (green) by repeatedly generating new motion plans in real-time. In each motion planning iteration, WAITR calculates a reachable set (blue and purple) for the contact wrench between the manipulator and the object as well as a Forward Reachable Set (FRS) for the whole manipulator system for a continuum of possible motion plans. The FRS is shown in purple in a) for a single planning iteration. WAITR solves a constrained trajectory optimization problem to find a collision-free motion in this FRS that does not result in relative motion while making progress towards an intermediate waypoint (grey) and the global goal. Parts c)-e) show the contact constraints enforced during a hardware experiment for a single planning iteration.
Simulation Results
This video is a simulation trial performed to test WAITR against ARMOUR while manipulating a small cylinder and is one of the results reported in Tab. 2 of the paper.
This video is a simulation trial performed to test WAITR against ARMOUR while manipulating a tall champagne glass and is one of the results reported in Tab. 2 of the paper.
This video is a set of simulation trials performed to test the effect of trajectory parameters on the performance of WAITR. The parameterized trajectories rely on a parameter \(\eta_{j,1}\) which encodes the range of possible final joint positions of the robot at the end of a planning iteration. Changing this parameter affects the joint velocity and joint acceleration. A larger range of \(\eta_{j,1}\) means that the range of possible joint velocities and joint accelerations are all larger.
The following table reports the results of 100 simulation trials for four different ranges of \(\eta_{j,1}\). The average planning time is the average time to find a solution per planning iteration. Note that WAITR requires a new solution within one second. The joint speed in degrees per second \((^{\circ}/s)\) is reported, as well as the percent increase for settings 2-4 compared with setting 1.
- For setting 1, the range of \(\eta_{j,1}=\frac{\pi}{72}\) for all joints.
- For setting 2, the range of \(\eta_{j,1}=\frac{\pi}{48}\) for all joints.
- For setting 3, the range of \(\eta_{j,1}=\frac{\pi}{32}\) for the first three joints, starting from the base joint, and \(\eta_{j,1}=\frac{\pi}{72}\) for the last for joints.
- For setting 4, the range of \(\eta_{j,1}=\frac{\pi}{32}\) for all joints.
| \(\eta_{j,1}\) Setting | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Goals Reached | 91 | 82 | 80 | 59 |
| Safe Stops | 9 | 18 | 20 | 41 |
| Avg. Plan Time (s) | 0.50 | 0.93 | 0.98 | 0.99 |
| Joint 1 Speed \((^{\circ}/s)\) | 0.81 | 1.05 \((30\%)\) | 1.22 \((50\%)\) | 1.87 \((130\%)\) |
| Joint 2 Speed \((^{\circ}/s)\) | 0.87 | 1.12 \((30\%)\) | 1.25 \((44\%)\) | 1.89 \((118\%)\) |
| Joint 3 Speed \((^{\circ}/s)\) | 0.68 | 0.85 \((25\%)\) | 0.92 \((34\%)\) | 1.41 \((107\%)\) |
| Joint 4 Speed \((^{\circ}/s)\) | 0.85 | 1.10 \((29\%)\) | 0.93 \((9\%)\) | 1.81 \((112\%)\) |
| Joint 5 Speed \((^{\circ}/s)\) | 0.79 | 1.04 \((33\%)\) | 0.86 \((9\%)\) | 1.52 \((93\%)\) |
| Joint 6 Speed \((^{\circ}/s)\) | 0.85 | 1.12 \((32\%)\) | 0.93 \((10\%)\) | 1.77 \((109\%)\) |
| Joint 7 Speed \((^{\circ}/s)\) | 0.77 | 1.06 \((35\%)\) | 0.89 \((13\%)\) | 1.53 \((95\%)\) |
The trajectory parameter simulation experiment illustrates the sensitivity of WAITR on the trajectory parameterization. The results show that as the range of \(\eta_{j,1}\) increases, the speed of the joints increases, but the computation time per planning iteration also increases because the size of the decision variable space also increases. We would like to highlight the allotted planning time for WAITR is one second, and if the planning time exceeds that, a brake maneuver is executed because a new trajectory has not been found in time. The manipulator system is allowed to plan for the next trajectory and can continue moving if one is successfully found. However, if a new trajectory cannot be found for 5 iterations in a row, we call this a safe stop. Due to the average planning time increasing with an increase in the range of \(\eta_{j,1}\), the number of safe stops increases as well. Therefore, the parameter \(\eta_{j,1}\) must be tuned to ensure desired results, such as decreasing the number of safe stops or moving faster.
This video is another scenario where a fetch robot is used to manipulate a block. A pybullet environment is used, which allows the block to be dropped into place on the tray and have the pybullet physics engine simulate the interaction between the block and tray throughout the trajectory. The example of a failure is due to the contact constrainsts being turned off:
Hardware Results
The overview video above shows the hardware experiments that are referenced in the paper.
This video is another scenario where the robot uses a straight-line high level planner which selects waypoints along a straight line in joint space between the current configuration and the goal. The first part shows an example of a failure due to contact constrainsts being turned off, then it shows a success when contact constraints are turned on. Both scenarios use the same global start and goal, as well as the same straight line high level planner.
Related Projects
- Autonomous Robust Manipulation via Optimization with Uncertainty-aware Reachability
- Safe Planning for Articulated Robots Using Reachability-based Obstacle Avoidance With Spheres
Citation
This project was developed in Robotics and Optimization for Analysis of Human Motion (ROAHM) Lab at University of Michigan - Ann Arbor.
@article{brei2024waiter,
author={Brei, Zachary and Michaux, Jonathan and Zhang, Bohao and Holmes, Patrick and Vasudevan, Ram},
journal={IEEE Robotics and Automation Letters},
title={Serving Time: Real-Time, Safe Motion Planning and Control for Manipulation of Unsecured Objects},
year={2024},
volume={9},
number={3},
pages={2383-2390},
keywords={Robots;Trajectory;Manipulators;Real-time systems;Uncertainty;Planning;Optimization;Manipulation planning;robot safety;collision avoidance},
doi={10.1109/LRA.2024.3355731}}